factorise by grouping 14x^3-35x^2 18x-45= 0 factor by grouping

there are 3 red,1 blue,and 2 yellow marbles in a bag.once a marble is selected,it is not replaced.find the probability.p(red and then yellow)p(2 red marbles in a row)

scientific notation form for 0.2x10^6?

What is the volume of 19.87 mol of ammonium chloride (NH4Cl) at STP?

How many atoms are in 131.97 liters of water vapor at STP?

how many atoms are in 131.97 liters of water vapor at stp?

What is the expected freezing point of a 0.80 m solution of CaCl2? (Assume complete dissociation.)

it takes 15 minutes to do 1 chart. how many hours to do 15,200 charts?

Convert y=2x^2-12x-7 into vertex from of a parabola.

how are alkaline earth metals pepared?

11 square root of 119 + 11 square root of 119

Suppose that degree is an angle in standard position whose terminal side intersects the unit circle at (15/17, -8/17). Find the exact values of Tan degree ,Cos degree , and Sec Degree .

find the integration of sinx.cosx dx lower limit - 3pi/4 upper limit pi/4

find the integration of e^-x/ (1- e^-2x)dx or ∫e^-x/ (1- e^-2x)dx upper limit ln 2 root 3 lower limit ln 2

the graph of f , f` and f`` are shown on the same set of coordinate axes . Idenity each graph . Explain there reasoning ?

In a optical inspe ction system is to distinquish among different parts types . The probabiltiy of a correct classificatiobn of any part is 0.98 …….. A Binomial B Geometric C hypergeometric D poission E none of these

find the given higher - order derivative f```(x) = 2x^1/2 f^4(x) or f```(x) = 2root (x) f^4(x)

Twelve sheep were fed a special diet consisting of dried grass and barley for three 2. months. At the end of the period the plasma insulin concentration (U/ml) was determined for each sheep. The data are as follows:20.5 26.2 18.8 21.2 22.1 21.6 25.4 26.8 22.9 22.8 30.8 28.4 What does the IQR explain about the distribution of the plasma insulin concentration of the twelve sheep?, c) Five number summary. Also construct the boxplot for the above data set.

"Twelve sheep were fed a special diet consisting of dried grass and barley for three 2. months. At the end of the period the plasma insulin concentration (U/ml) was determined for each sheep. The data are as follows:20.5 26.2 18.8 21.2 22.1 21.6 25.4 26.8 22.9 22.8 30.8 28.4 Calculate the following:a) First (Q1) and third (Q3) quartiles, b) The interquartile range (IQR). "

What are the two main source of genetic variation ? Which of them is more common ?

list the five conditions necessary to maintain genetic equilibrium in a population ?

Why might a geographic barrier such as a large river cause the formation of a new species of small rodents but nor a new species of the birds ?

Are the members of a population necessarily the same species ? Explain

calculate the PH of a solution formed by mixing 85 ml of 0.13 M lactic acid with 95 ml of 0.15 M sodium lactate. (K HLaC =1.4 * 10^-4)

Ans:- 

this is a buffer soluton of lactice acid and its conjugate base 

          moles of salt = 95*0.15  

                               = 14.25 mili moles 

reaction of salt 

          NaC₃H₅O_{3 <--->} Na+    +  C₃H₅O_{3 -} 

               [C₃H₅O_3-]= 14.25 mili moles

          moles of acid = 85*0.13 

                                 = 11.05 mili moles 

Henderson Hasselbalch equation for a weak acid

                            pH = Pka  +  log ([A¯] / [HA])

so formula change to 

                          pH = Pka  +  log ([ C₃H₅O₃¯] / [C₃H₆O₃])

plug the value in formula, we get 

                         pH = - log KHlac   +  log 14.25/11.05

                         pH = - log 1.4 * 10^-4  +  log 14.25/11.05

use calculator to solve these values, we get 

                         pH = 3.85+ 0.11

                         pH =3.96

Answer = pH of solution is 3.96  

In this problem we have learned

find DE where FE= 35.2 , DE= 31.7 and angle FED = 49 degree ? 2 adjacent sides and angle formed by them is given Find the third side of triangle

find out the special right triangle, find the side BC in the given triangle ? Angle = 45 degree , side = 4 cm

graph each linear equation in two variable. Find at least five solutions in your table of values for each equation. y = 1/3x -1 and y=-5/2x +1

graph each linear equation in two variable. Find at least five solutions in your table of values for each equation. y = 1/3x -1 and  y=-5/2x +1

Answer :- 

In first equation  y  = 1/3x -1 the cofficient of x is 1/3 

so plug the value multiply of 3 so plug x = 0,-3,+3,-6,+6 we get 

x	(x/3) -1
0	-1
-3	-2
3	0
-6	-3
6	1

in second equation  y=-5/2x + 1 the cofficient of x is -5/2 here 2 is in denominator 

so plug the value x multiple of 2 so plug x = 0 ,-2 ,  2,  4, -4 

x	(-5/2)*x +1
0	1
2	-4
-2	6
4	-9
-4	11

now use these values to draw the graph 

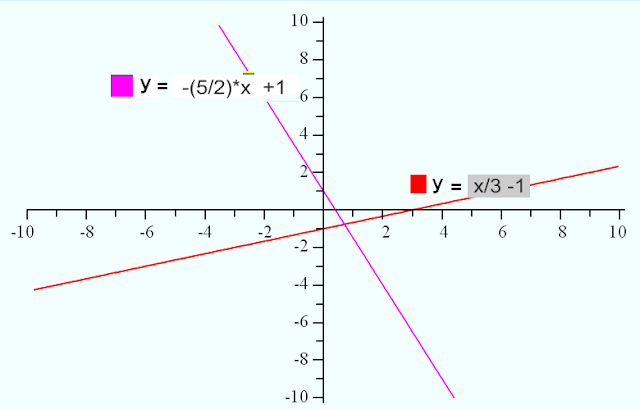graph each linear equation in two variable. Find at least five solutions in your table of values for each equation. y = 1/3x -1 and  y= -5/2x +1

with help of this problem you can easily under stood 

How to solve graph the linear equations ?

how to find the solution table for the equaions ?

how to draw the graph using equations?

explain why the line (x,y,z) = (4,-5,2) + t (2,1,0) is parallel to xy plane

 (x,y,z) = (4,-5,2)  + t (2,1,0)

 here (4,-5,2) is the point and direction is 2i + j + 0k 

as the cofficient of direction of z axis is 0 

so the line is parallel to xy plane 

explain why the line (x,y,z) = (4,-5,2)  + t (2,1,0)  is parallel to xy plane

derivative of sin(sin(sinx))

derivative of sin(sin(sinx)), example of chain rule, how to solve a chain rule problem?, solve the derivative using the chain rule 

derivative of sin(sin(sin x))

use formula of chain rule 

                                      =>d/dx (sin y) = cos y * dy/dx

               the value of y= sin (sin x) 

use above formula we get  
                                    => cos (sin (sinx))*d/dx (sin(sin x))

    now new value of  y = sinx 

use above formula again we get 
                                     => cos (sin (sin x))* cos(sin x) * d/dx sin x 

now use the same formula again we get 
                                     => cos (sin (sin x))* cos(sin x) * cos x 

Answer =  cos (sin (sin x))* cos(sin x) * cos x